Cuentos, símbolos y matemática

Diana M. Benavides Bohórquez y Juan Carlos Londoño Rojas

Licenciados en Matemáticas y Física, docentes del colegio Alas, en Jamundí, Valle del Cauca (Colombia); y participantes de la formación en Cuentoterapia. En el año 2020 crearon el blog Matemáticas sin dificultad para acercar conocimientos elementales a la gente común y compartir metodologías de aprendizaje. https://matematicassindificultad-escrita.blogspot.com/

Antes de entrar de lleno en el tema del artículo, me gustaría iniciar contando que fue una sorpresa recibir la invitación para escribir en esta revista. Entre los meses de mayo y junio de 2020 participamos en las clases magistrales ofrecidas a través de la plataforma Zoom por Lorenzo Hernández, Carmen González y Francisco Jorquera. Hablamos de algunos cuentos, desentrañando su simbología y, por ende, su conexión con las cartas del Tarot de los cuentos. Durante dichos encuentros, mientras se realizaba el análisis de cada historia, algunas de las ideas que escuchaba mostraban una relación con símbolos pertenecientes al mundo de las matemáticas, que generaban en mí una sensación de esas que uno no puede explicar y que me llevaron, con un poco de susto y con el impulso de mi pareja, a pedir la palabra dentro del gran grupo de participantes y preguntar aquello que por mi mente rondaba, dado que no era la primera vez que veía que los cuentos y las matemáticas, de algún modo, se conectaban. Mis intervenciones fueron escuchadas por el editor de esta revista, quien decidió contactarme y hacerme la propuesta de escribir un artículo para la revista, y sin pensarlo mucho acepté la invitación. Pero no podía hacerlo solo, por lo que lo primero que tenía que preguntar para escribir el texto era si mi compañera de vida podría intervenir también. ¿Por qué? Sencillamente porque Diana y yo hemos recorrido un camino donde nuestros animus y anima se complementan de una manera muy especial, y juntos podemos hacer algo mejor.

Sin querer robarle protagonismo a aquello en lo que más adelante vamos a profundizar, me parece importante comenzar a hilar lo que nos trae hasta acá. Diana y yo nos conocimos en la Facultad de Física de la Universidad del Valle, en Cali (Colombia), por el año 2003. Con los años, fuimos desarrollando una linda amistad que una década después, mientras nos graduábamos como licenciados en Matemáticas y Física, terminó por convertirse en una relación más formal. Nuestro campo de formación tiene algo en particular: es muy afín a la mente y muy distanciado del corazón. En nuestra cultura, tener conocimientos en estas áreas es sinónimo de inteligencia y grandeza; nada más ajeno a la realidad, pues hemos venido comprendiendo que la grandeza no viene de la cabeza, sino de la interacción equitativa que tiene con el corazón y la acción.

Trabajamos en distintos colegios, mientras que nuestras búsquedas, generadas muchas veces por situaciones adversas del día a día, nos iban llevando por un camino de transformación interior que tomó fuerza con nuestra llegada al Colegio Alas, donde laboramos en la actualidad. Gracias a María del Pilar Jaramillo y Hertzel Behar, dueños del colegio en mención, se nos abrió la puerta para que, a través de Francisco, Lorenzo y Carmen, en momentos cronológicamente distintos, pudieran visitarnos y presentarnos el mundo de la cuentoterapia. De este modo conocimos a estos seres maravillosos que nos deslumbraron con su generosidad, conocimientos, simpatía y amor por los cuentos.

El Tarot de los cuentos maravillosos de la península ibérica, desplegado durante el taller realizado en Medellín, Colombia

Debido a lo anterior, ahora nos sentimos maravillados por los cuentos y por su capacidad de quedarse en el inconsciente, armonizando recuerdos y sanando el alma (decimos esto a partir de nuestra experiencia). Pero debemos contar que al principio fuimos escépticos con aquello que esta herramienta simbólica nos ofrecía, puesto que hemos evidenciado que las mentes racionales y, más aún, con formación estructurada en los campos de estudio de las matemáticas y la física, suelen estar alerta, poner resistencia y dar poca importancia cuando se habla de trabajo personal o crecimiento interior; solo se acepta aquello que pueda ser medido y probado a través del método científico o demostrado por medio de la lógica y la argumentación. Con esta armadura mental encima, que nos generaba cierta reserva frente al tema, iniciamos nuestro primer taller de cuentoterapia, donde prontamente nuestros esquemas mentales se fueron disolviendo para abrir paso al niño interior que se escondía tras dicha armadura. Fuimos seducidos por la belleza que mostraban los cuentos narrados, donde los elementos simbólicos que aparecían describían diversas personalidades, incluyendo las nuestras, dando paso a un mar de emociones que estaban escondidas y que comenzaban a reclamar su lugar. Desde entonces, y teniendo en cuenta que Diana realizó su trabajo de grado con un análisis de Alicia a través del espejo, de Lewis Carroll, los cuentos se convirtieron en una nueva herramienta para continuar con nuestro proceso de crecimiento interior, siendo capaces de encontrar una forma de reconciliar a la mente y el corazón para darnos la oportunidad de andar más livianos en el viaje de la vida y así poder apreciar y disfrutar el camino.

Como se mencionó, en nuestros talleres iniciales habíamos notado que en los cuentos aparecían elementos matemáticos que llamaban nuestra atención, pero que podrían pasar desapercibidos, puesto que los símbolos y números hacen parte de la cotidianidad. He aquí donde nos enfocamos en el eje principal de este artículo, para referirnos a los símbolos a través de un campo de estudio cuyo lenguaje es totalmente simbólico. Motivados por estas relaciones, hablábamos entre los dos sobre la relevancia de las matemáticas como camino de evolución de la conciencia, tomando como referente un fragmento del diálogo entre Sócrates y Glaucón que encontramos en Reinhardt (2007, p. 17): “Date cuenta, pues, amigo mío, que esta ciencia parece sernos realmente indispensable, porque es evidente que obliga al alma a utilizar la pura inteligencia para alcanzar la verdad en sí”. Con base en este texto, notamos que en la modernidad se ha perdido un poco la conexión entre esta rama de estudio con lo espiritual, y teniendo presente que, si bien, la matemática nació como una necesidad del hombre para contar, también pensamos que lo hizo para exteriorizar los anhelos de su alma; un alma que busca encontrar su lugar en el universo; tal vez así lo entendió el gran astrónomo Galileo Galilei cuando expreso: “La filosofía [natural] está escrita en ese grandísimo libro que tenemos abierto ante los ojos, quiero decir, el universo, pero no se puede entender si antes no se aprende a entender el lenguaje, a conocer los caracteres en los que está escrito. Está escrito en lenguaje matemático y sus caracteres son triángulos, círculos y otras figuras geométricas, sin las cuales es imposible entender ni una palabra; sin ellos es como girar vanamente en un oscuro laberinto” *1.

A partir de esa conversación, encontramos una relación entre los cuentos más antiguos y una de las ramas más importantes y simbólicas de las matemáticas: la geometría. Por ejemplo, hallamos una primera conexión y es la que tiene cada ser humano con la parte femenina (el círculo) y masculina (la recta). Nos explicaremos más a fondo. El círculo (el cual construimos con la ayuda del compás), representa lo femenino, puesto que son estas curvas cerradas y, en general, lo curvo, lo que nos conecta con la creación (recordemos la forma del vientre materno). No solo obtenemos otras figuras a partir de esta, como estrellas con diversos números de puntas y flores que salen a partir de las particiones equidistantes en el círculo; o los polígonos regulares que tienen la misma longitud en cada lado. El círculo también nos conecta con la creación desde lo simbólico, mediante la división tangible entre un espacio interno y otro externo; que puede representar nuestro ser exterior (por fuera de nosotros: lo que el mundo tiene para brindarnos) y nuestro ser interior (dentro de nosotros: conciencia, sentimientos y emociones). Es como un entrelazamiento de dos mundos que coexisten en cada persona. Por otra parte tenemos la recta, que representa lo masculino. Para poder trazarla necesitamos la ayuda de una regla, y con ellas podemos construir figuras que contienen lados iguales o desiguales y que dan continuidad a la creación. Con las rectas se pueden realizar diversas construcciones, pero algo hermoso que tienen es que dos rectas se pueden encontrar en un punto (intersección) y cada una seguir su camino; pueden reflejarse; pueden no encontrarse nunca (paralelas), o pueden existir en una sola (superpuestas). Si se tienen tres rectas, se pueden ubicar dos de ellas de forma paralela y poner una transversal para formar ángulos correspondientes: alternos internos, alternos externos u opuestos por el vértice.

De izquierda a derecha, figuras 1.a (Creación con círculos y rectas), 1.b (Creación con hilos para obtener un círculo a partir de segmentos), 2 (Flor de la vida) y 3 (Tetraedro). Autores: Diana M. Benavides Bohórquez y Juan Manuel Catacoli, egresado del colegio Atlas (1b).

Si bien se puede ver cada figura por separado, como se explicó en el párrafo anterior, lo bello que tiene el conjunto del círculo y de la recta, es que con los dos se pueden construir las más hermosas y armónicas figuras. Por ejemplo, en la figura 1.a observamos una estrella de seis puntas inscritas en un hexágono, la cual se obtuvo a partir de círculos y luego, desde cada centro, se trazaron todas las posibilidades de segmentos formando el cubo de Metatrón. Según Beutel (2015, p. 71): “En la mitología judía, Metatrón —quien tiene la misión de poner en práctica el proyecto divino en la realidad tridimensional— es uno de los ángeles que se encuentran en lo más alto de la jerarquía celestial”. Esta figura se pintó de manera intercalada con el color negro para destacar las simetrías y, aunque se noten más las rectas (lo masculino), se obtiene a partir de círculos que simbolizan lo femenino. En la figura 1.b observamos un círculo realizado con técnica de hilos. Las veinticuatro puntillas que bordean el círculo con igual distancia entre ellas, representan los segmentos; y una puntilla en la mitad representa el centro. El hilo se entrelaza en las puntillas y se sigue una secuencia con varias capas para que la figura se pueda notar. Esta última figura nos muestra cómo, a partir de lo recto, se puede llegar a lo circular. También se pueden obtener figuras como los polígonos regulares (figuras planas o en dos dimensiones) y los sólidos platónicos (figuras tridimensionales). Al tener sus lados iguales, estos le regalan al ser una sensación de equilibrio; y con la flor de la vida (figura 2), la visión del inicio de la existencia. Los cinco sólidos platónicos tienen una conexión con el pensamiento filosófico y están conectados con cada elemento que nos rodea: el tetraedro contiene cuatro caras triangulares y representa el fuego (figura 3); el hexaedro contiene seis caras cuadradas iguales y representa la tierra (figura 4); el octaedro contiene ocho caras triangulares iguales y representa el aire (figura 5); el icosaedro contiene veinte triángulos iguales y representa el agua (figura 6); y el dodecaedro contiene doce caras pentagonales iguales y se relaciona con el éter (figura 7); Beutel (2015, p. 73) menciona que las tres primeras figuras descritas se relacionan con el número cuatro. Este número representa, desde lo matemático, los cuatro puntos espaciales y las cuatro dimensiones; mientras que, simbólicamente hablando, según el Diccionario de los símbolos de Jean Chevalier y Alain Gheerbrant (2017, p. 421): “El cuatro simboliza lo terreno, la totalidad de lo creado y de lo revelado”. Las otras dos figuras se conectan con el número cinco, un número que se relaciona con la vida misma. En el Diccionario de los símbolos (2017, pp. 322-323) se explica que el cinco es la suma del primer número par (2) y del primer número impar (3); y que, entre los nueve primeros números naturales, se ubica en la mitad, y por ello es “el número del centro, la armonía y el equilibrio”. Para los pitagóricos, el número cinco era sagrado porque representaba el matrimonio. Cinco son también los sólidos platónicos, que geométricamente se obtienen trazando segmentos a partir de la flor de la vida, que a su vez es una figura que contiene diecinueve círculos. El primero es el central y alrededor de este se trazan seis círculos; posteriormente se trazan doce, como se aprecia en la figura 2.

De izquierda a derecha, figuras 4 (hexaedro), 5 (octaedro), 6 (icosaedro) y 7 (dodecaedro). Dibujadas por Diana M. Benavides Bohórquez.

Motivados por las experiencias vividas en el colegio y gracias a la gestión de las directivas de este, pudimos asistir y participar del taller “La búsqueda del alma” dirigido por Lorenzo y programado por EIDEP, en la ciudad de Medellín, Colombia. Para este taller, Lorenzo traía una compañía especial, pues al darle inicio de sus pertenencias sacó el recién publicado Tarot de los cuentos maravillosos de la península ibérica. Al revisar las cartas, vimos que La Emperatriz (femenino) recibe el número 3, y El Emperador (masculino) recibe el número 4, pero entre estos dos arcanos aparecía una carta muy particular, que es La Transmutación y recibe el número PI (π). Esta carta muestra una bella conjunción entre lo masculino y lo femenino, no solo por su posición en la baraja, sino también por el cuento que la acompaña: “El oricuerno”.

En este punto, nos vemos en la necesidad de hacer un paréntesis para revisar lo siguiente: matemáticamente, Π (Pi) es un número irracional, que a su vez es un decimal infinito que no repite una secuencia de cifras entre sí, y por tanto no se puede expresar como una fracción. Podríamos decir que en este conjunto numérico también encontramos todas las raíces que no tienen un valor exacto. Para comprender mejor el concepto matemático de un número irracional, es necesario recordar que en un inicio solo se reconocían los números naturales (N), que son los números con los que podemos contar indefinidamente en un solo sentido a partir del uno. Luego, se introducen los números enteros (Z) como una necesidad, entre otras cosas, para contar a partir de un punto de referencia, tanto lo que se tiene como también lo que se debe. Dicho conjunto numérico es bellísimo, porque nos deja ver los números naturales como si se reflejaran en un espejo representado por el número cero (espejo que juega un rol importante en diversos relatos). Además, podemos relacionarlos con las distintas polaridades existentes en el ser humano, muy presentes en el desarrollo de la personalidad de algunos protagonistas importantes de los cuentos. Posteriormente, en el desarrollo histórico de las matemáticas, surgió la necesidad de explicar lo que pasaba si se partía la unidad en diferentes trozos, dando paso a las fracciones, compuestas por números enteros. De estos, a su vez, se obtienen cierto tipo de números decimales con los que podemos operar fácilmente, y a los que llamamos números racionales (Q).

Cuando todo parecía estar resuelto, escondidas en estas particiones aparecieron otro tipo de números cuya cifra decimal no se podía terminar de contar, y como en el caso del número de oro, esta cifra traía consigo armonía, belleza y perfección. Son estos los números irracionales, que históricamente aparecen con los pitagóricos. Al tratar de medir la hipotenusa de un triángulo rectángulo isósceles *2, cuyos catetos miden una unidad, estos encontraron un valor que no podían explicar: √2 (raíz cuadrada de dos)... y cuenta la historia que el número de oro fue descubierto por el escultor griego Fidias (siglo V a.c.). Más adelante, los números irracionales explican la completitud de “la recta numérica”. Para hacernos una idea, dado que el proceso matemático es un poco más complejo, esto es como si tuviéramos una cuerda infinita conformada por conjuntos numéricos, pero aún llena de incontables huecos. Los números irracionales aparecen para tapar dichos espacios infinitos y darle una forma completa a esta cuerda.

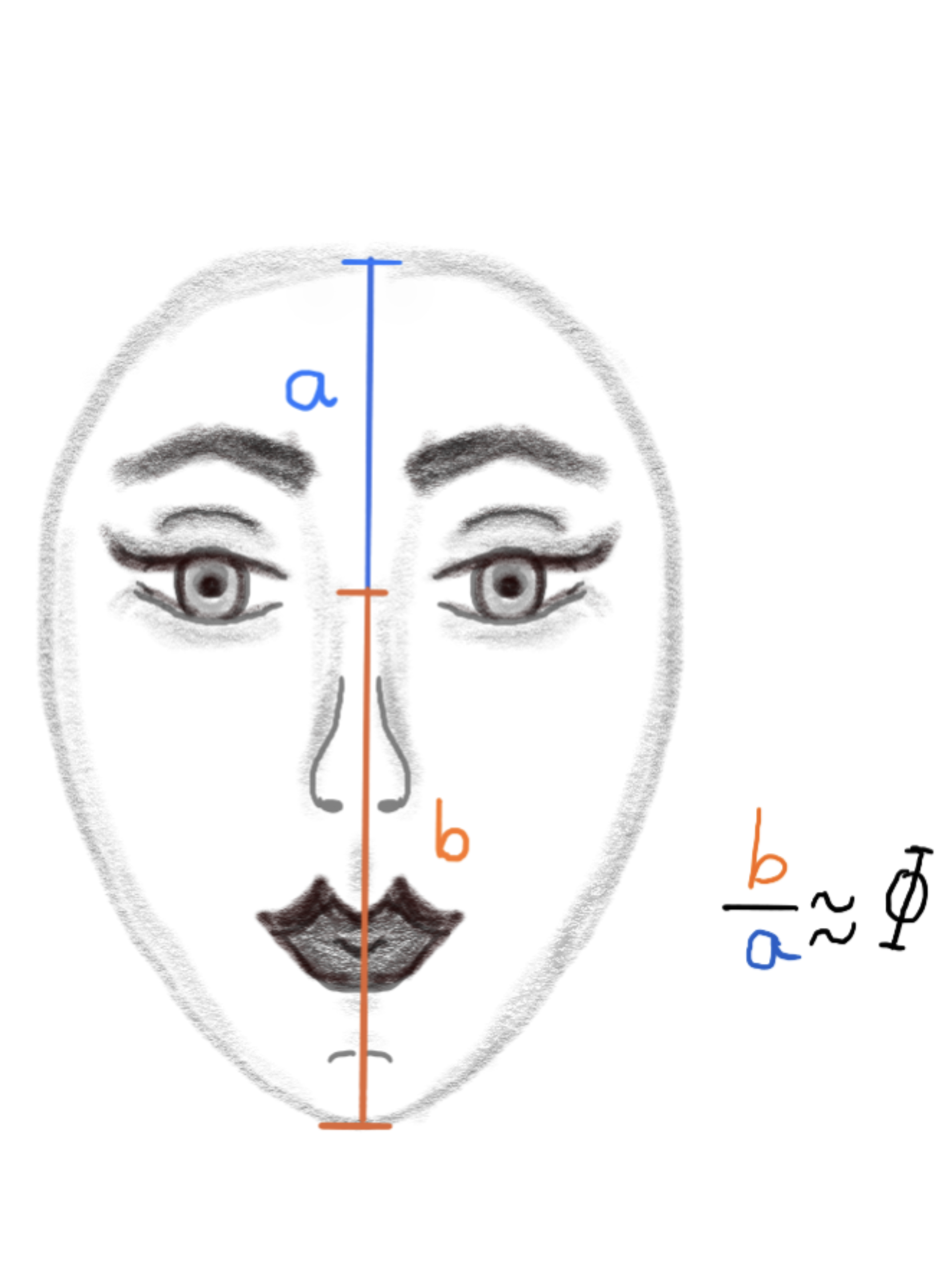
Después de conocer el Tarot de los cuentos, durante los tres días que duró el taller nos enfocamos en el análisis de La reina de las nieves. Con este cuento nos sentimos particularmente identificados, puesto que, a medida que avanzaba la historia, descubríamos un Kay que quería resaltar frente a los otros por su habilidad mental, enfocada en unos buenos conocimientos de “aritmética, quebrados y geometría”. El cuento nos mostraba, de manera paralela, un relato de nuestra propia vida y la de aquellos que, junto a nosotros, decidieron enfocarse por el mundo de las ciencias exactas; sacrificando un poco el valor del corazón para darle total fuerza a su capacidad intelectual. Analizábamos con los demás participantes del taller, bajo la orientación de Lorenzo, los párrafos que nos adentraban en la historia, la cual mantenía un fuerte simbolismo matemático. Como en el momento en que la vieja peinaba a Gerda con un “peine áureo, y los cabellos de la niña se rizaban y brillaban como hebras de oro en torno a su linda carita, que era redonda y fresca como una rosa”. Estas líneas hacen una posible alusión a la proporción áurea, mencionada antes como el número de oro (que es aproximadamente 1,61803389...). Este número lo podemos encontrar en nuestro cuerpo, en la naturaleza, en esculturas y obras arquitectónicas, pues sale de una división entre una parte más pequeña a y una parte más grande b, pero de tal forma que a y b pertenecen al mismo segmento. Así, por ejemplo, si nos ubicamos en nuestro rostro y medimos la distancia que hay desde la parte más alta de la frente (justo donde comienza el cabello) hasta la altura de las pupilas, y luego desde este último punto hasta el mentón, tenemos dos medidas que al dividirlas (la más grande sobre la más pequeña) nos dan un valor aproximado al número de oro, como se observa en la figura 8. Entonces podremos decir que, al cumplir esta medida, somos matemáticamente bellos.

figura 8. Aproximación al número de oro en el rostro

Cuando se habla de proporción áurea se habla también del pentágono, que es un polígono regular de cinco lados, que por ende nos lleva a una estrella de cinco puntas. El número cinco lo vemos en nuestro cuerpo: dos brazos, dos piernas y una cabeza; en nuestras manos, cada una con cinco dedos; también en la parte delantera del rostro, con los cinco orificios (dos ojos, dos fosas nasales y la boca), como lo menciona Beutel en su libro La flor de la vida en ti (2015, p. 83). El pentágono también aparece en los pétalos de algunas flores y se dice que era el “código secreto” de los pitagóricos, quienes, al estudiarlo encontraron relaciones que conllevarían al desarrollo de la escala musical. La proporción áurea, con la que se puede obtener el número de oro, se relaciona también con la sucesión de Fibonacci. Esta serie de números naturales va dando números que son el resultado de la suma de los dos anteriores, es decir, comenzamos con 1, luego 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8 y así se tiene esta famosa sucesión que va hasta el infinito. Observemos su conjunto: {1, 2, 3, 5, 8, 13, 21, 34, 55...}. La sucesión de Fibonacci puede verse en las plantas y en general en la naturaleza, por supuesto desde lo finito, pues en la realidad las figuras o formas que vemos tienen un inicio y un fin. Lo mágico de los números de dicha sucesión es que si tomamos cualquier número del anterior conjunto y lo dividimos por su antecesor, obtendremos un valor aproximado al del número de oro: Fn+1/Fn, por ejemplo: 2/1 = 2, 3/2 = 1.5, 5/3 = 1.66..., 8/5 = 1.6, 13/8 = <1.625, 21/13 = 1.615384..., 34/21 = 1.619047..., 55/34 = 1.617647... Observemos que, a medida que se avanza con los números tomados dentro del conjunto de la sucesión, el valor del resultado es más aproximado al número de oro.

fig. 9. Relación entre la forma de la rosa y la sucesión de Fibonacci

Volviendo al cuento, desde un punto de vista matemático podríamos pensar que el autor, al escribir sobre la carita de la niña, hace referencia a la proporción áurea y a lo femenino; y que más allá del peine que utiliza la abuela, quiere resaltar particularmente las medidas de la cara. Y también la rosa, un símbolo que en el taller destacamos, dado que podría hacer referencia al “amor presente y el amor perdido”, que es lo que Gerda manifiesta por Kay al salir en su búsqueda. La rosa es una flor que cumple con el número de oro, pero a partir de la espiral de Fibonacci, como se observa en la figura 9. Asimismo, cabe destacar uno de los elementos fundamentales de la historia: el espejo que trata de reparar Kay, uniendo los “cien millones de billones de partículas”. Lo hacemos por el tamaño de la cifra en mención y por otras nociones que están implícitas en las cualidades de dicho espejo, tales como simetría, oposición, punto de referencia, imagen real e imaginaria equidistantes; todas estas aplicables al conjunto de los números enteros. Los espejos y lentes se estudian desde la física con modelos matemáticos y eso nos daría para escribir otro artículo; por lo pronto podemos decir que el espejo nos da la noción de que hay algo que esta detrás funcionando a la inversa y a la misma distancia que el cuerpo original que se refleja, tal y como funcionan los números reales (excepto los naturales).

Antes de que Gerda logre llegar a aquel castillo de nieve donde se encuentra atrapado Kay, el cuento alude de manera implícita a algunos números, que queremos destacar para finalizar este relato. Un ejemplo lo encontramos cuando el reno pide a la mujer finesa que dé a Gerda “la fuerza de doce hombres”. Y otro cuando se hace alusión a los copos de nieve, copos que al ser observados a través de un microscopio forman figuras de tipo hexagonal (polígonos de 6 lados), como se observa en la figura 10. Si hemos leído el cuento, recordaremos que al comienzo del segundo episodio la abuela dice a Kay y a Gerda que los copos de nieve son “abejas blancas que juegan en el aire”. Las colmenas tienen formas hexagonales y esto permite que sus lados encajen entre sí de manera perfecta, sin pérdida de espacio; creando una estructura más resistente que además se adapta mejor al cuerpo de las abejas, cosa que no ocurriría con el triángulo y con el cuadrado. Estas figuras no son tan perfectas para las abejas porque la anatomía de estos animalitos haría que las proporciones fuesen diferentes, y no se optimizaría el espacio. Podríamos preguntarnos entonces porqué ellas no utilizan círculos completos. La respuesta es simple. Aunque el círculo se puede adaptar a sus cuerpos, al no poder llenar el espacio completamente, no resulta una estructura tan resistente. Siempre quedarán vacíos. Esto último ocurre también con los pentágonos y otros polígonos.

De izquierda a derecha, figura 10 (cubo de Metatrón) y cristales de nieve de seis puntas

Para tener un referente de la forma hexagonal podemos ver la figura 1.a, cuyo polígono sale a partir de dibujar la flor de la vida. El número seis sale a partir de la suma de los primeros tres números naturales: 1 + 2 + 3 = 6, y obtenemos el mismo resultado si multiplicamos los tres números: 1 × 2 × 3 = 6. De esta manera vemos que en el seis aparecen implícitos los números 1, 2 y 3, cada uno con su símbolo. El seis para los pitagóricos simbolizaba la unión de lo masculino con lo femenino, y era para ellos el primer número perfecto y el tercer número triangular. El primer número triangular es el uno y el segundo es el tres. Reciben este nombre porque se simbolizan con puntos, que van acomodándose hasta formar un triángulo equilátero.

El número 12, mencionado antes cuando recordamos qué clase de brebaje pedía el reno para Gerda, es el resultado de 2 × 6. Si seis es un número perfecto para los pitagóricos y mágico por la belleza que encierra el hexágono, el doce será el doble de todo eso. Por eso creemos que Andersen lo usa para describir una fuerza capaz de vencer a la Reina de las nieves: la fuerza de doce hombres. El doce también simboliza la fuerza porque está relacionado con el sólido platónico que representa el éter, el prana, el chakra espiritual, la ascensión y el misterio. Para elogiar la sabiduría de la mujer finlandesa, el reno dice que ella puede atar todos los vientos del mundo con un hilo, y que si deshace el tercero y el cuarto nudos se desatará una tempestad. Estas palabras nos indican que hay una relación entre el número tres y el cuatro, que puede dar se por medio de una suma o de una multiplicación. Como un poco después aparece el número doce deducimos que se trata de una multiplicación. En el Diccionario de los símbolos (Tomo I) de Jean Chevalier y Alain Gheerbrant (2017, pp. 465-468) encontramos que el doce es “acción y movimiento”, “la multiplicación de un cuadrado y un triángulo” donde el cuadrado es el cuatro y el triángulo es el tres. Consultando este diccionario reconocimos, además, que hay otra forma de ver el número cuatro: por medio de las dimensiones que conocemos actualmente (espacio: ancho, altura y profundidad, y tiempo), o de los cuatro elementos (tierra, aire, fuego y agua) o de los cuatro puntos cardinales (norte, sur, este y oeste). Y hay otras formas de ver el tres, como la representación de la santísima trinidad (padre, hijo y espíritu santo) o de los tres principios alquímicos (azufre, sal y mercurio) o de las tres fases (sólido, líquido y gaseoso) o de los tres planos del mundo (alto, ancho y espesor). Nos llamó particular atención que en el cuento se nombre el agua en sus tres estados: sólido (el hielo), líquido (el río) y gaseoso (cuando la niña hablaba y salía vapor de su boca). Creemos que, al hacerlo, el autor guarda de manera implícita el número tres.

figura 11. Toroide en tres dimensiones. Autora: Diana Mª Benavides Bohórquez

Después de retomar muchos conceptos matemáticos y aplicarlos a la lectura de La reina de las nieves, y después de contar lo que encontramos en el diccionario de símbolos de Chevalier y en el libro de Beutel sobre la Flor de la vida, llegamos a una figura matemática llamada anillo tórico o toroide (figura 11). La describimos como un anillo porque su centro es hueco, así sea infinitamente pequeño. Está compuesto por doce círculos: seis iniciales (como en la Flor de la vida) y seis secundarios, de tal manera que el centro de los secundarios se ubica en las mitades de los círculos anteriores. Como se observa en la figura 12c, esto refleja el inicio de la espiral, formando seis alas. A esta figura se la conoce como espiral del anillo tórico o espiral primigenia, debido a los trazos circulares en secuencia. Fue utilizada como símbolo del eterno movimiento por muchas culturas del mundo; por ejemplo, aparece grabada en unas piedras conservadas en la isla sueca de Gotland, tal como menciona Beutel en el libro citado (2015, p. 48).

Retomando la figura del anillo tórico, añadimos que los círculos pueden ir aumentando hasta el doble de lo anterior, es decir, que podemos tener otra espiral de veinticuatro círculos; la siguiente sería de cuarenta y ocho, y así sucesivamente. Así pudimos llegar a una generalización de la fórmula, para obtener una cantidad x de círculos, pétalos o espirales, donde n representa la cantidad de vueltas de círculos que daremos (n = 0, 1, 2, 3,….). Cuando tomamos n = 0 se obtienen los seis círculos iniciales de la figura, que es de donde se parte. Esta generalización la obtuvimos a partir de la geometría aplicada en un programa que se llama GeoGebra. Solo usamos la ecuación para saber cuántos círculos trazar según la cantidad de vueltas que deseamos dar, pero no es para expresarla en el plano cartesiano como una gráfica que relaciona dos variables. Esta fórmula posiblemente ya existe y ha sido patentada por algún matemático, aunque no encontramos referencia alguna. Quisimos anotarla en este artículo porque, además de relacionar los números dos y tres, se puede representar gráficamente o dibujar, para hacer alusión a la relación entre los números seis y doce. Al dibujarla y pintarla nos llevamos una gran sorpresa, y es que dependiendo de dónde y cómo se aplique el color, asimismo se verá la figura. A continuación presentamos el anillo tórico coloreado de diversas formas, dando un efecto visual como si se tratase de distintas figuras (se puede observar en las figuras 12 a, b, c y d). También es importante aclarar que, en sí, el anillo tórico es una figura tridimensional, y que desde el dibujo la observamos desde la perspectiva plana, es decir, desde arriba de la figura. Como puede verse a partir de lo dicho en este artículo, en los cuentos aparecen muchos elementos, y pueden tratarse desde diversos puntos de vista: entre ellos, el de las matemáticas.

De izquierda a derecha, figuras 12.a (anillo tórico en color), 12.b (anillo tórico en blanco y negro), 12.c (anillo tórico destacando la espiral) y 12.d (anillo tórico formando seis anillos entrelazados) . Autora: Diana Mª Benavides Bohórquez

Notas

1* Tomado del sitio web https://institucional.us.es/blogimus/2017/04/galileo-y-lasmatematicas-del-universo/

2* Es un triángulo con un ángulo recto, cuyos dos catetos tienen la misma longitud y la hipotenusa, que es el lado de mayor medida.

Bibliografía

Beutel, A. (2015). La flor de la vida en ti. Barcelona: Ediciones Obelisco.

Reinhardt, A. E. (2007). Des-cifrar, la matemática en la escuela (Vol. II). Buenos Aires, Argentina: Editorial Antroposófica.

Jorquera F.,Pallarés, L.,Gómez, L.(2019). Tarot de los cuentos. Murcia, España. Edición La Diligente.

Chevalier, J., Gheerbrant A. (2017). Diccionario de los símbolos (Vols. I & II). Bogotá, Colombia: Editorial Solar.

Este artículo fue publicado originalmente en la primavera de 2021, en el número 6 de la revista anual de AICUENT.